1. 개념 설명
(1) 다익스트라는 그래프의 한 정점에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘이다.
( 이것을 줄여서 최단 경로 알고리즘이라고 부른다. )
(2) 다익스트라는 그래프 방향의 유무는 상관없으나, 간선들 중 단 하나라도 가중치가 음수이면
이 알고리즘은 사용할 수 없다.
(3) 만약 음의 가중치를 가지는 간선이 있으며 가중치 합이 음인 사이클이 존재하지 않는 경우 벨만-포드
알고리즘을 사용한다.
( 또한 그래프 내에 가중치 합이 음인 사이클이 존재한다면, 무한히 음의 사이클을 도는 경우 합이 음수
무한대로 발산하기 때문에 최단 경로를 구성할 수 없다. )
2. 과정
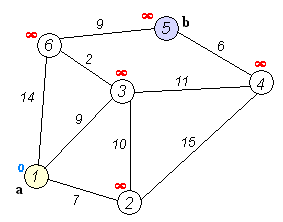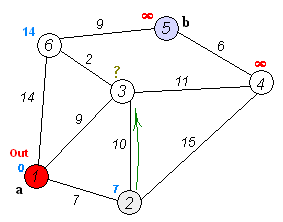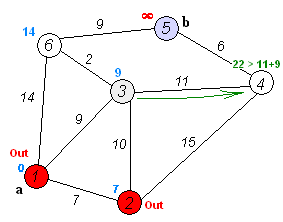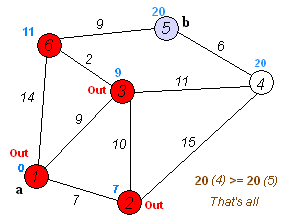
- 실제로 수행되는 과정이며, 특정한 정점에서 다른 모든 정점으로 가는 최단 경로를 기록하고 있다.
3. 입출력 조건 및 예제
입력 조건
(1) 첫째 줄에 정점의 개수 V와 간선의 개수 E, 시작 정점의 번호 K가 주어진다.
(3) 두 번째 줄부터 E개의 줄에 걸쳐 각 간선을 나타내는 세 개의 정수 (u, v, w)가 순서대로 주어진다.
출력 조건
(1) 최단 경로의 경로값들을 출력한다.
( 시작점 자신은 0으로 출력하고, 경로가 존재하지 않는 경우에는 INF를 출력하면 된다. )
입력 예제
|
6 9 1
1 2 7
1 3 9
1 6 14
2 3 10
2 4 15
3 4 11
3 6 2
4 5 6
6 5 9
|
출력 예제
|
[2147483647, 0, 7, 9, 20, 20, 11]
|
4. 코드
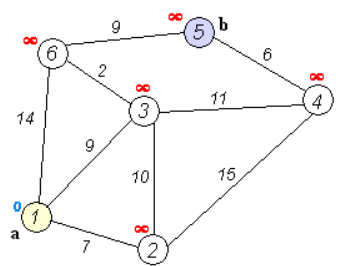
( 아래의 코드는 위 그래프 그림을 보고 작성되었으며 같이 보면서 코드를 보는 것을 추천한다. )
|
class Node implements Comparable<Node>{
int E, W;
public Node(int E, int W) {
this.E = E;
this.W = W;
}
@Override
public int compareTo(Node o) {
// TODO Auto-generated method stub
return this.W - o.W;
}
}
public class Test {
static int V, E, K;
static ArrayList<Node>[] list;
static int[][] map;
static boolean[] visited;
static int[] dist;
static BufferedReader sc = new BufferedReader(new InputStreamReader(System.in));
static StringTokenizer st;
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws IOException {
StringTokenizer st = new StringTokenizer(sc.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
list = new ArrayList[V+1];
dist = new int[V+1];
visited = new boolean[V+1];
Arrays.fill(dist, Integer.MAX_VALUE);
for(int i=1; i<=V; i++) {
list[i] = new ArrayList<>();
}
for(int i=1; i<=E; i++) {
st = new StringTokenizer(sc.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
list[u].add(new Node(v, w));
}
solve(K);
System.out.println(Arrays.toString(dist));
}
static void solve(int start) {
PriorityQueue<Node> queue = new PriorityQueue<>();
queue.add(new Node(start, 0)); // 시작 정점과 시작 가중치 0을 넣는다.
dist[start] = 0;
while(!queue.isEmpty()){
Node curNode = queue.poll();
start = curNode.E;
if(visited[start]) continue;
visited[start] = true;
for(Node node : list[start]){
if(dist[node.E] > dist[start] + node.W){
dist[node.E] = dist[start] + node.W;
queue.add(new Node(node.E, dist[node.E]));
}
}
}
}
}
|
cs |
5. 시간 복잡도
(1) 인접 행렬: O(N^2)
(2) 인접 리스트: O(N+logN)
( 이때, V는 정점, E는 간선을 의미한다. )
6. 장점
(1) 다익스트라 알고리즘은 벨만-포드 알고리즘에 비해 좀 더 효율적이기 때문에, 그래프가 큰 경우에도
사용할 수 있다.
7. 단점
(1) 위에서도 말했지만 다익스트라 알고리즘은 음수인 가중치를 가진 간선이 있는 겨웅에는 사용할 수 없다.
8. 관련 문제 풀어보기
1238번: 파티 (골드 3) (tistory.com)
1238번: 파티 (골드 3)
1238번: 파티 (acmicpc.net) 1238번: 파티 첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000), X가 공백으로 구분되어 입력된다. 두 번째 줄부터 M+1번째 줄까지 i번째 도로의 시작점, 끝점, 그리고 이 도로를 지
kind-coding.tistory.com
1753번: 최단 경로 (골드 4) (tistory.com)
1753번: 최단 경로 (골드 4)
1753번: 최단경로 (acmicpc.net) 1753번: 최단경로 첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘
kind-coding.tistory.com
9. 참고 사이트
다익스트라(Dijkstra) 알고리즘 | 👨🏻💻 Tech Interview (gyoogle.dev)
다익스트라(Dijkstra) 알고리즘 | 👨🏻💻 Tech Interview
다익스트라(Dijkstra) 알고리즘 다익스트라 알고리즘은 특정한 정점에서 다른 모든 정점으로 가는 최단 경로를 기록한다. 여기서 DP가 적용되는 이유는, 굳이 한 번 최단 거리를 구한 곳은 다시 구
gyoogle.dev
'알고리즘 (with JAVA) > 기본 알고리즘' 카테고리의 다른 글
| BFS (Breadth First Search) (0) | 2023.05.05 |
|---|---|
| DFS (Depth First Search) (0) | 2023.05.05 |
| 해시 테이블 (Hash Table) (0) | 2023.05.01 |
| 이진 탐색 (Binary Search) (0) | 2023.04.29 |
| 계수 정렬 (Counting Sort) (0) | 2023.04.29 |