1. 개념 설명
(1) DFS는 깊이 우선 탐색으로 트리나 그래프에서 한 루트로 탐색하다가 특정 상황에서 최대한 깊숙이 들어가서
확인한 뒤 다시 돌아가 다른 루트로 탐색하는 방식이다.
(2) DFS는 스택 또는 재귀 함수로 구현할 수 있으며, 모든 경로를 방문해야 할 경우 사용에 적합하다.
2. 과정
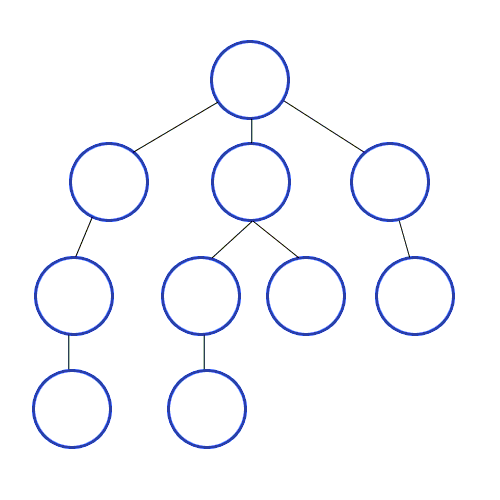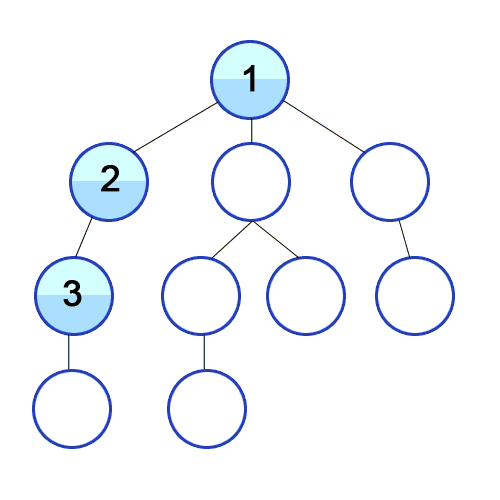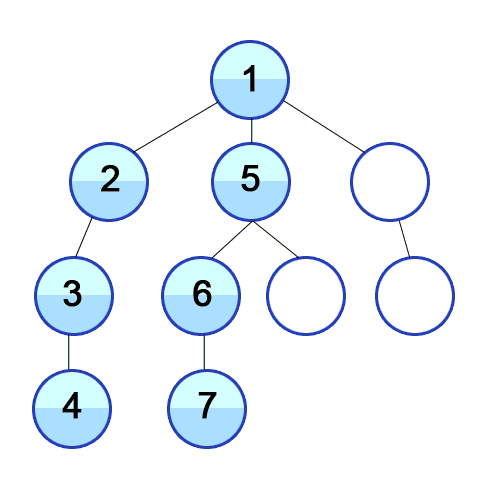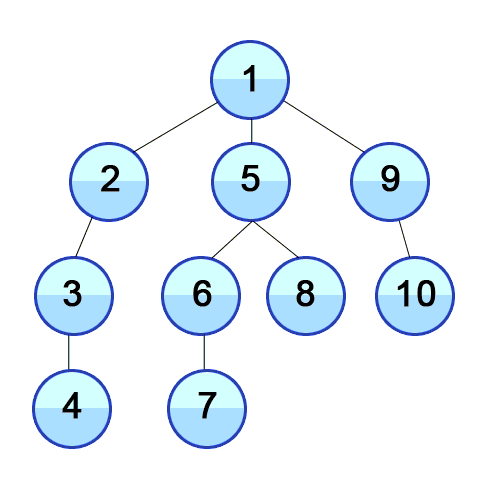
- 실제로 수행되는 과정이며, 하나의 브랜치 조사가 다 끝나면 다시 다른 브랜치를 조사하고 있다.
3. 인접 행렬 vs 인접 리스트

(1) 인접 행렬 (Adjecency Matrix)
: 2차원 배열에 각 노드가 연결된 형태를 기록하는 방식이다.
( 만약 위와 같은 그래프가 있다고 한다면, 아래와 같이 2차원 배열을 사용한다. )
Graph = {
{0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 0},
{0, 1, 0, 0}
};( 연결되었다면 0, 그렇지 않으면 1이다. )
( 예를 들어, Graph[1][1] 또는 Graph[2][3]은 0이므로 연결되지 않았다는 표현이다. )
(2) 인접 리스트 (Adjecency List)
: 모든 노드에 연결된 노드들의 정보를 차례대로 기록하는 방식이다.
( 만약 위와 같은 그래프가 있다고 한다면, 아래와 같이 2차원 배열을 사용한다. )
Graph = {
{},
{2, 3},
{1,3,4},
{1,2},
{2}
};
4. 코드
: DFS는 일반적으로 일반 재귀(dfs_Recursion)와 스택 재귀(dfs_StackRecursion) 두 가지로 구현할 수 있다.

( 아래의 코드 (1)과 (2)는 위 그래프 그림을 기반으로 코드를 작성했다. )
(1) 인접 행렬
|
public class DFS_Matrix {
static boolean[] visited = new boolean[9]; // 0을 제외한 그래프에서 1~8 중에 방문 했는지 체크하는 변수
static int[][] graph = {
{},
{0, 0, 1, 1, 0, 0, 0, 0, 1},
{0, 1, 0, 0, 0, 0, 1, 0, 1},
{0, 1, 0, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 1, 0, 1, 0},
{0, 0, 0, 1, 1, 0, 0, 1, 0},
{0, 0, 1, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 1, 0, 0, 0},
{0, 1, 1, 0, 0, 0, 0, 0, 0}
}; // 인접 행렬 그래프이며, 0행과 0열은 모두 0으로 비어두었다.
static Stack<Integer> stack = new Stack<>();
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) {
// 시작 지점은 1로 가정한다.
dfs_Recursion(1);
System.out.println();
visited = new boolean[9];
// 시작 지점은 1로 가정한다.
dfs_StackRecursion(1);
}
static void dfs_Recursion(int nodeIndex) {
// 시작 노드 또는 해당 인덱스 노드를 방문 처리
visited[nodeIndex] = true;
// 방문 노드 출력
System.out.print(nodeIndex + " -> ");
for(int i=1; i<=8; i++) {
if(graph[nodeIndex][i] == 1 && !visited[i]) {
dfs_Recursion(i);
}
}
}
static void dfs_StackRecursion(int nodeIndex) {
// 노드 추가 및 방문 처리
stack.push(nodeIndex);
visited[nodeIndex] = true;
// 스택 내용 출력
System.out.println(stack);
for(int i=1; i<=8; i++) {
if(graph[nodeIndex][i] == 1 && !visited[i]) {
dfs_StackRecursion(i);
// 더이상 방문할 곳이 없다면 호출했던 노드로 다시 돌아가기
stack.pop();
System.out.println(stack);
}
}
}
}
|
cs |
(2) 인접 리스트
|
public class DFS {
static boolean[] visited = new boolean[9]; // 0을 제외한 그래프에서 1~8 중에 방문 했는지 체크하는 변수
static int[][] graph = { {}, {2,3,8}, {1,6,8}, {1,5}, {5,7}, {3,4,7}, {2}, {4,5}, {1,2}}; // 0을 제외한 해당 인덱스 노드의 인접한 노드 리스트
static Stack<Integer> stack = new Stack<>();
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) {
// 시작 지점은 1로 가정한다.
dfs_Recursion(1);
System.out.println();
visited = new boolean[9];
// 시작 지점은 1로 가정한다.
dfs_StackRecursion(1);
}
static void dfs_Recursion(int nodeIndex) {
// 시작 노드 또는 해당 인덱스 노드를 방문 처리
visited[nodeIndex] = true;
// 방문 노드 출력
System.out.print(nodeIndex + " -> ");
for(int node : graph[nodeIndex]) {
//인접한 노드가 방문한 적이 없다면 DFS 수행
if(!visited[node]) dfs_Recursion(node);
}
}
static void dfs_StackRecursion(int nodeIndex) {
// 노드 추가 및 방문 처리
stack.push(nodeIndex);
visited[nodeIndex] = true;
// 스택 내용 출력
System.out.println(stack);
for(int node : graph[nodeIndex]) {
if(!visited[node]) {
dfs_StackRecursion(node);
// 더이상 방문할 곳이 없다면 호출했던 노드로 다시 돌아가기
stack.pop();
System.out.println(stack);
}
}
}
}
|
cs |
5. 시간 복잡도
(1) 인접 행렬: O(V^2)
(2) 인접 리스트: O(V+E)
( 이때, V는 정점, E는 간선을 의미한다. )
6. 장점
(1) 단지 현 경로상의 노드들만 기억하면 되므로 저장 공간의 수요가 비교적 적다.
(2) 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다.
7. 단점
(1) 해가 없는 경로에 깊이 빠질 가능성이 있다.
( 이럴때는 미리 지정한 임의 깊이까지만 탐색하도록 한다. )
(2) 얻어진 해가 최단 경로가 된다는 보장이 없다.
( 즉, 목표 해에 이르는 경로가 다수인 문제에서 DFS는 해를 찾으면 탐색을 끝내버리므로, 최적의 경로가 아닐수도
있다는 의미이다. )
8. 관련 문제 풀어보기
-> 풀이는 아래의 링크로 가면 된다.
1260번: DFS & BFS (실버 2) (tistory.com)
9. 참고 사이트
'알고리즘 (with JAVA) > 기본 알고리즘' 카테고리의 다른 글
| 다익스트라 (Dijkstra) (0) | 2023.05.05 |
|---|---|
| BFS (Breadth First Search) (0) | 2023.05.05 |
| 해시 테이블 (Hash Table) (0) | 2023.05.01 |
| 이진 탐색 (Binary Search) (0) | 2023.04.29 |
| 계수 정렬 (Counting Sort) (0) | 2023.04.29 |