1. 개념 설명
(1) BFS는 너비 우선 탐색으로 최대한 깊숙이 들어가서 탐색을 시작하는 DFS와는 달리 인접한 노드부터 먼저
탐색하는 방법이다.
( 아래 2. 과정을 통해 이해하자. )
(2) BFS는 재귀호출을 사용하는 DFS와는 달리, 자료구조 큐(Queue)를 사용하는 경우가 일반적이다.
( 그러므로, 3. 코드에서는 큐를 이용한 BFS를 보여줄 것이다. )
2. 과정

- 실제로 수행되는 과정이며, 앞서 DFS(깊이 우선 탐색)과 BFS(너비 우선 탐색)을 비교하고 있다.
3. 코드
: BFS는 재귀를 사용하지 않고 일반적으로 큐를 통해 구현한다.
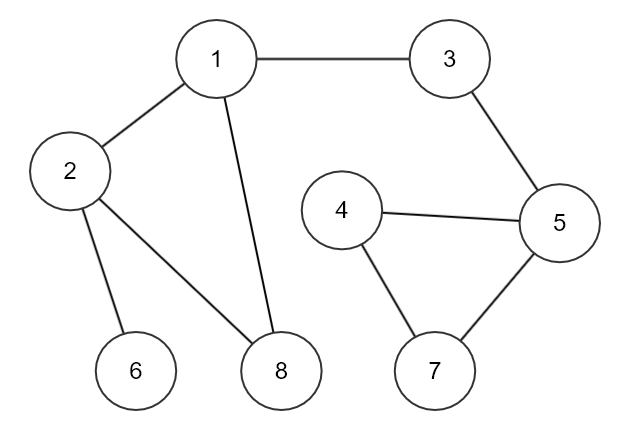
( 아래의 코드 (1)과 (2)는 위 그래프 그림을 기반으로 코드를 작성했다. )
(1) 인접 행렬
|
public class BFS_Matrix {
static Queue<Integer> q = new LinkedList<>();
static boolean[] visited = new boolean[9]; // 0을 제외한 그래프에서 1~8 중에 방문 했는지 체크하는 변수
static int[][] graph = {
{},
{0, 0, 1, 1, 0, 0, 0, 0, 1},
{0, 1, 0, 0, 0, 0, 1, 0, 1},
{0, 1, 0, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 1, 0, 1, 0},
{0, 0, 0, 1, 1, 0, 0, 1, 0},
{0, 0, 1, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 1, 0, 0, 0},
{0, 1, 1, 0, 0, 0, 0, 0, 0}
}; // 인접 행렬 그래프이며, 0행과 0열은 모두 0으로 비어두었다.
public static void main(String[] args) {
// 시작 지점은 1로 가정한다.
bfs(1);
}
static void bfs(int nodeIndex) {
// 시작 노드 또는 해당 인덱스 노드를 방문 처리
q.add(nodeIndex);
visited[nodeIndex] = true;
while(!q.isEmpty()) {
nodeIndex = q.poll();
// 방문 노드 출력
System.out.print(nodeIndex + " -> ");
for(int i=1; i<=8; i++) {
if(graph[nodeIndex][i] == 1 && !visited[i]) {
q.add(i);
visited[i] = true;
}
}
}
}
}
|
cs |
(2) 인접 리스트
|
public class BFS_List {
static Queue<Integer> q = new LinkedList<>();
static boolean[] visited = new boolean[9]; // 0을 제외한 그래프에서 1~8 중에 방문 했는지 체크하는 변수
static int[][] graph = { {}, {2,3,8}, {1,6,8}, {1,5}, {5,7}, {3,4,7}, {2}, {4,5}, {1,2}}; // 0을 제외한 해당 인덱스 노드의 인접한 노드 리스트
public static void main(String[] args) {
// 시작 지점은 1로 가정한다.
bfs(1);
}
static void bfs(int nodeIndex) {
// 시작 노드 또는 해당 인덱스 노드를 방문 처리
q.add(nodeIndex);
visited[nodeIndex] = true;
while(!q.isEmpty()) {
nodeIndex = q.poll();
System.out.print(nodeIndex + " -> ");
for(int i=0; i< graph[nodeIndex].length; i++) {
int node = graph[nodeIndex][i];
if(!visited[node]) {
q.add(node);
visited[node] = true;
}
}
}
}
}
|
cs |
4. 시간 복잡도
(1) 인접 행렬: O(V^2)
(2) 인접 리스트: O(V+E)
( 이때, V는 정점, E는 간선을 의미한다. )
5. 장점
(1) 만약 여러 갈래 중 무한한 길이를 가지는 경로가 존재하고 탐색 목표가 다른 경로에 존재한다면, DFS의 경우
계속 무한한 길이의 경로에서 영원히 종료하지 못하지만 BFS는 모든 경로를 동시에 진행되기 떄문에 탐색이
가능하다.
(2) BFS는 가중치가 모두 똑같은 그래프에서 시작점과 끝점이 주어진다면, 최단 경로를 알아낼 수 있다.
6. 단점
(1) 경로가 매우 길 경우에는 탐색 가지가 급격히 증가함에 따라 보다 많은 기억 공간을 필요로 하게 된다.
(2) 해가 존재하지 않은 유한 그래프인 경우 모든 그래프를 탐색한 후에서야 실패로 끝난다.
7. 관련 문제 풀어보기
-> 풀이는 아래의 링크로 가면 된다.
1260번: DFS & BFS (실버 2) (tistory.com)
8. 참고 사이트
'알고리즘 (with JAVA) > 기본 알고리즘' 카테고리의 다른 글
| 다익스트라 (Dijkstra) (0) | 2023.05.05 |
|---|---|
| DFS (Depth First Search) (0) | 2023.05.05 |
| 해시 테이블 (Hash Table) (0) | 2023.05.01 |
| 이진 탐색 (Binary Search) (0) | 2023.04.29 |
| 계수 정렬 (Counting Sort) (0) | 2023.04.29 |