1. 개념 설명
(1) 계수 정렬은 데이터의 개수(예를 들면 1이 두 개 있다면 2)를 데이터의 값에 대응하는 위치에 저장한 뒤,
자신의 위치에서 앞에 있던 값을 모두 더한 배열을 만든 뒤, 거기서 데이터가 들어가야 할 위치를 찾아내는
알고리즘이다.
(2) 계수 정렬은 가장 큰 데이터에 따라 효울이 좌지우지 된다.
2. 과정
|
1. 정렬해야 할 배열을 탐색하여 그 최댓값을 구한다.
( 여기서는 주어진 배열 A를 사용한다. )
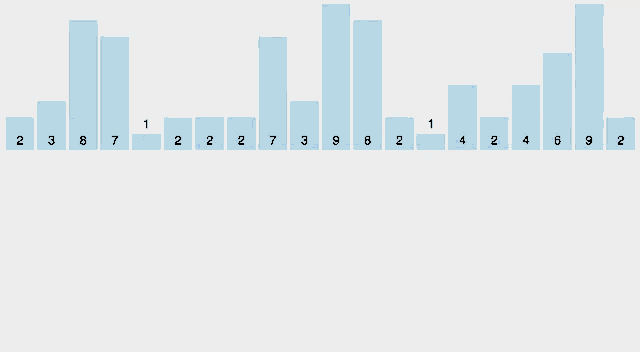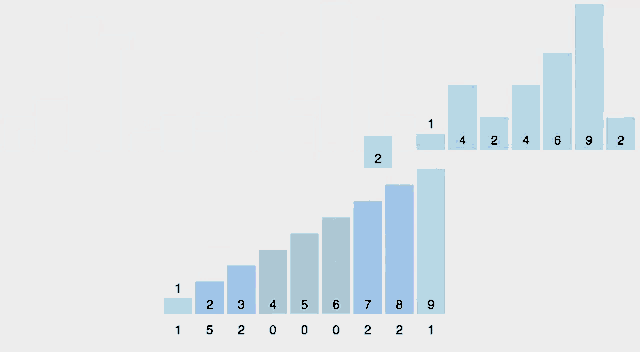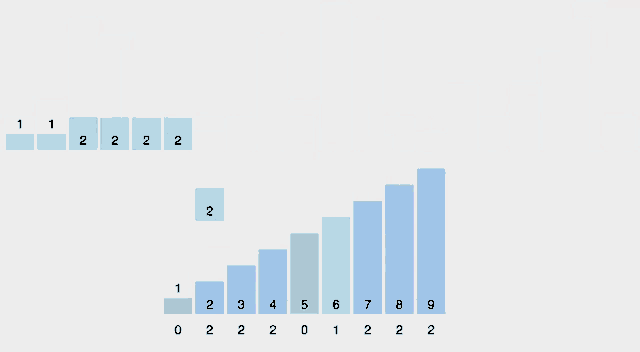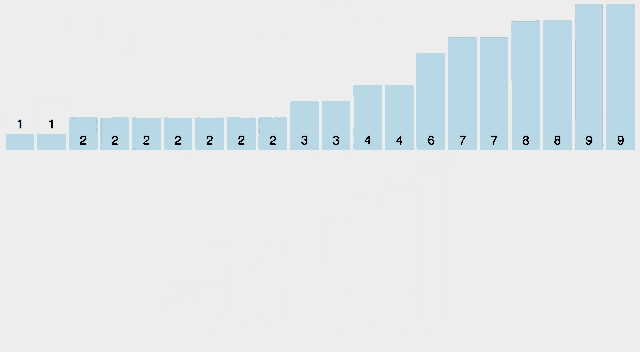
A = [5, 4, 1, 3, 2, 5, 1]
최댓값 K = 5;
2. K+1 만큼의 크기로counts 배열을 생성한다.
counts = [0, 0, 0, 0, 0, 0]
3. A 배열 모든 원소에 대하여 각 대응되는 인덱스 위치에 ++를 해준다.
counts = [0, 2, 1, 1, 1, 2]
( 이때, count[i]는 배열 A에 i가 몇 개 있는지를 의미한다. )
4. counts[i] += counts[i-1]을 하여 누적 counts 배열을 만들어준다.
counts = [0, 2, 3, 4, 5, 7] ( 이때, count[i]는 배열 A에 i 이하의 원소가 몇 개 있는지를 의미한다. )
5. 정렬된 배열을 담기 위한 ans배열을 A배열 크기만큼 만든다.
ans = [0, 0, 0, 0, 0, 0, 0]
6. counts의 A[i]에 대응하는 원소를 찾아서 --를 해준다.
int value = A[i]
counts[value]--
7. 준비된 ans 배열에 counts[value]의 값 인덱스 위치를 찾아 value를 넣어준다.
ans[counts[value]] = value
8. 6~7의 과정을 남아 있는 자료에 대하여 반복한다.
|
cs |
3. 코드
|
public class CountingSort {
private static int[] A = new int[50];
private static int[] counts = new int[31]; // 수의 범위 0~30
private static int[] ans = new int[A.length];
public static void main(String[] args) {
// 랜덤값 생성
for(int i=0; i<A.length; i++) {
A[i] = (int)(Math.random()*31);
}
System.out.println("정렬 전: " + Arrays.toString(A));
countingSort();
System.out.println("정렬 후: " + Arrays.toString(ans));
}
public static void countingSort() {
for(int i=0; i<A.length; i++) {
counts[A[i]]++;
}
for(int i=1; i<counts.length; i++) {
counts[i] += counts[i-1];
}
for(int i=0; i<A.length; i++) {
int value = A[i];
counts[value]--;
ans[counts[value]] = value;
}
}
}
|
cs |
4. 시간 복잡도
(1) 계수 정렬의 시간 복잡도는 O(N+K)이다. 이때, K는 데이터의 최댓값을 의미한다.
5. 공간 복잡도
(1) 주어진 배열 안에서 정렬이 일어나므로, 공간 복잡도는 O(N+K)이다.
6. 장점
(1) 데이터의 최댓값인 K가 매우 작다면, 선형 시간의 효과를 볼 수 있다.
7. 단점
(1) 데이터의 최댓값인 K가 억 단위로 넘어간다면, 아무리 데이터 개수 N이 작다고 하더라도 동작 시간이
커질 수 밖에 없다.
'알고리즘 (with JAVA) > 기본 알고리즘' 카테고리의 다른 글
| 해시 테이블 (Hash Table) (0) | 2023.05.01 |
|---|---|
| 이진 탐색 (Binary Search) (0) | 2023.04.29 |
| 기수 정렬 (Radix Sort) (0) | 2023.04.29 |
| 힙 정렬 (Heap Sort) (0) | 2023.04.29 |
| 삽입 정렬 (Insertion Sort) (0) | 2023.04.27 |