+1-1 Techinque
- 아래와 같은 문제가 있다.
| 1차 수직선 상에서 가로 n개의 선분이 주어졌고 어떤 임의의 세로 수직선을 그었을 때, 만나는 서로 다른 선분의 개수는? |

| 답: 3개 |
- 그림을 통해 봤을 때 당연히 3개라는 것은 알 수 있지만, 이를 컴퓨터로 구현하기 위해서는 어떻게 해야 할까?
- 바로 1차 선분의 시작점과 끝점에 각각 +1과 -1을 붙이는 것이다.

- 시작점과 끝점의 가중치 값을 부여하고 빨간선 앞쪽에 있는 가중치 값들 모두 더해주면 답이 나오게 된다.
- 이 점을 활용하면 주어지는 모든 선분 N개를 각각 2개의 시작점, 끝점으로 구분하여 총 2N개의 점으로 나눠 이를 x좌표 순으로 오름차순 정렬한 뒤, x = k보다 커지기 직전까지의 숫자를 전부 더하는 식으로 진행해볼 수 있다.
- 구현 방법에는 2가지가 존재하며, 좌표의 범위에 따라 나뉜다.
구현 방법 (1) - 좌표 범위가 작을 때
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
class Segment {
int x1, x2;
public Segment(int x1, int x2){
this.x1 = x1;
this.x2 = x2;
}
};
public class Main {
public static void main(String[] args) {
Segment[] segments = new Segment[]{
new Segment(1, 5),
new Segment(4, 7),
new Segment(3, 6),
new Segment(5, 10),
new Segment(9, 13),
new Segment(8, 15),
new Segment(12, 16),
};
int n = 7;
int k = 11;
// 주어진 좌표의 범위가 작을 때에는
// 배열을 이용하여 직접 각 칸에
// +1 -1을 진행해도 무방합니다.
int[] checked = new int[21];
for(int i = 0; i < n; i++) {
int x1 = segments[i].x1;
int x2 = segments[i].x2;
checked[x1] += 1;
checked[x2] -= 1;
}
// x = k 전까지
// 각 위치에 적혀있는 숫자들의 합을 구해줍니다.
int sumVal = 0;
for(int i = 1; i < k; i++)
sumVal += checked[i];
// x = k에 겹쳐져 있는 선분의 수 = 2
System.out.println(sumVal);
}
}
|
cs |
구현 방법 (2) - 좌표 범위가 클 때
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
|
import java.util.ArrayList;
import java.util.Collections;
class Segment {
int x1, x2;
public Segment(int x1, int x2){
this.x1 = x1;
this.x2 = x2;
}
};
class Point implements Comparable<Point> {
int x, v;
public Point(int x, int v){
this.x = x;
this.v = v;
}
@Override
public int compareTo(Point p) { // x 오름차순
return this.x - p.x;
}
};
public class Main {
public static void main(String[] args) {
Segment[] segments = new Segment[]{
new Segment(1, 5),
new Segment(4, 7),
new Segment(3, 6),
new Segment(5, 10),
new Segment(9, 13),
new Segment(8, 15),
new Segment(12, 16),
};
int n = 7;
int k = 11;
// 주어진 좌표의 범위가 큰 경우에는
// 각 선분을 두 지점으로 나눠서
// +1, -1로 담은 뒤,
// 정렬해줍니다.
ArrayList<Point> points = new ArrayList<>();
for(int i = 0; i < n; i++) {
int x1 = segments[i].x1;
int x2 = segments[i].x2;
points.add(new Point(x1, +1)); // 시작점
points.add(new Point(x2, -1)); // 끝점
}
// 정렬을 진행합니다.
// ArrayList에 대한 정렬에는 Collections를 이용합니다.
Collections.sort(points);
// x = k 전까지
// 각 위치에 적혀있는 숫자들의 합을 구해줍니다.
int sumVal = 0;
for(int i = 0; i < 2 * n; i++) {
int x = points.get(i).x;
int v = points.get(i).v;
// x가 k 이상이 되면 종료합니다.
if(x >= k)
break;
// 적혀있는 가중치를 전부 더해줍니다.
sumVal += v;
}
// x = k에 겹쳐져 있는 선분의 수 = 2
System.out.println(sumVal);
}
}
|
cs |
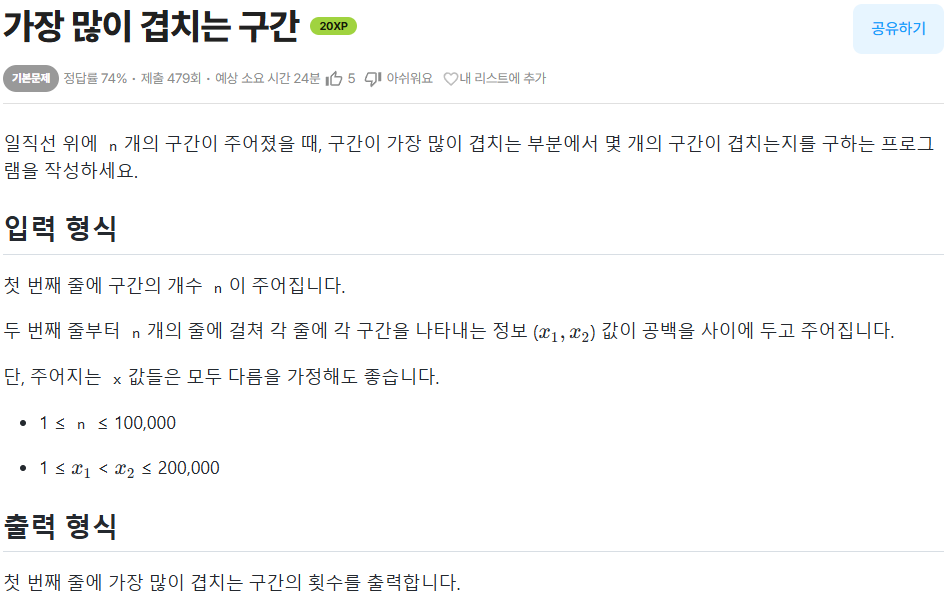
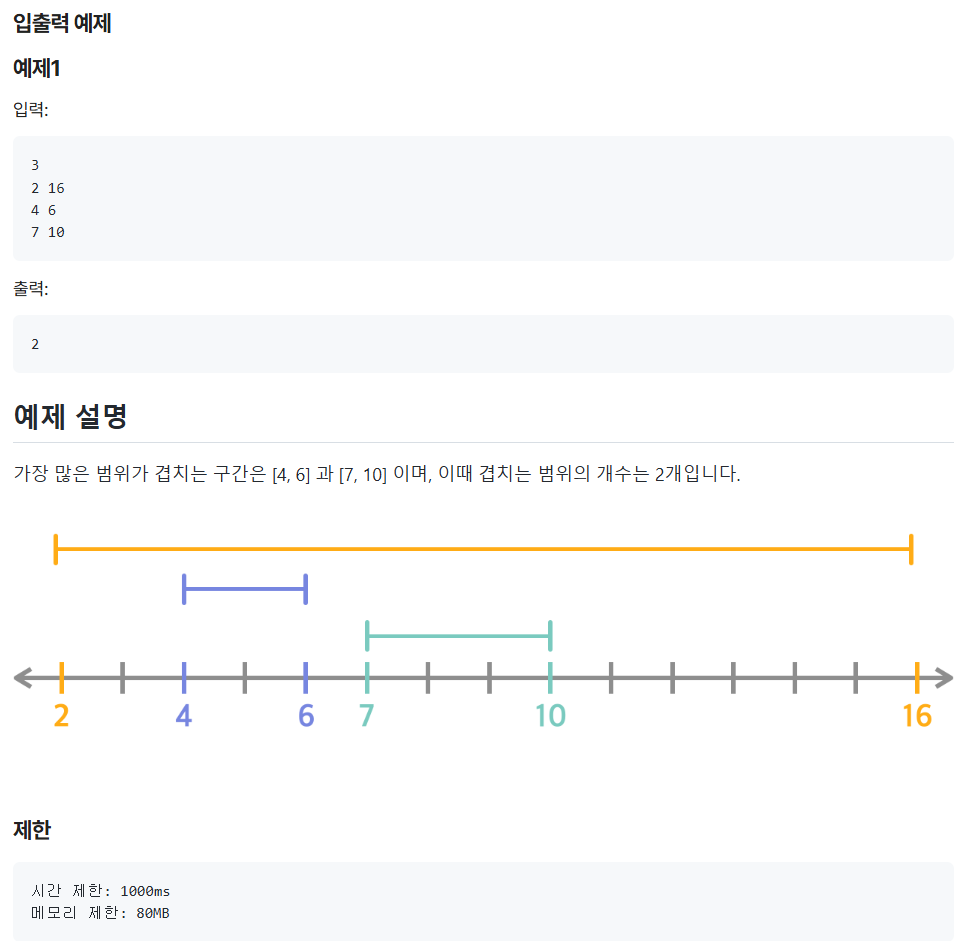
연습문제 - (코드트리) 가장 많이 겹치는 구간
[개념]가장 많이 겹치는 구간 | 알고리즘 기본 (codetree.ai)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
import java.util.*;
import java.io.*;
public class Main {
static int N, checked[], ans;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N = Integer.parseInt(br.readLine());
checked = new int[200001];
for(int i=1; i<=N; i++){
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
checked[x1]++;
checked[x2]--;
}
solve();
System.out.println(ans);
}
static void solve(){
int cnt=0;
for(int i=1; i<=200000; i++){
cnt += checked[i];
ans = Math.max(ans, cnt);
}
}
}
|
cs |

'알고리즘 (with JAVA) > 코드트리 조별과제' 카테고리의 다른 글
| 코드트리 조별과제 6회차 (8.19 ~ 8.25) (0) | 2024.08.19 |
|---|---|
| 코드트리 조별과제 5회차 (8.12 ~ 8.18) (0) | 2024.08.12 |
| 코드트리 조별과제 4회차 (8.05 ~ 8.11) (0) | 2024.08.06 |
| 코드트리 조별과제 3회차(7.29 ~ 8.04) (1) | 2024.08.03 |