1. 개념
- 동적 계획법은 큰 의미에서 분할 정복과 같은 접근 방식을 의미한다.
- 동적 계획법과 분할 정복의 차이는 문제를 나누는 방식에 있다.
- 동적 계획법에서의 어떤 부분 문제는 두 개 이상의 문제를 푸는 데 사용될 수 있기 때문에, 이 문제의 답을 여러 번
계산하는 대신 한 번만 계산하고 계산 결과를 재활용함으로써 속도의 향상을 꾀할 수 있다.
- 그렇게 하기 위해서는 이미 계산한 값을 저장해 둘 수 있는 캐시를 사용한다.
* 두 번 이상 계산되는 부분 문제를 중복되는 부분 문제(overlapping subproblems)라고 부른다.
2. 이해하기
- 동적 계획법 알고리즘을 이해하기 위해서 가장 유명한 이항 계수(binomial coefficient)의 계산을 예로
들어보겠다.
- 이항 계수는 아래의 그림처럼 서로 다른 n개의 원소 중에서 r개의 원소를 순서 없이 골라내는 방법의 수이다.

- 이항 계수는 아래의 그림처럼 점화식을 가진다.

( 이때, 점화식이란 재귀적으로 정의되는 수학적 함수를 의미한다. )
- 이 점화식을 이용하면 아래의 코드처럼 bino(n,r)을 얻을 수 있다.
|
int bino1(int n, int r) {
if(r==0 || n==r) return 1;
return bino(n-1, r-1) + bino(n-1, r);
}
|
- 이 함수 호출 과정을 아래의 그림을 보면 중복된 계산이 있는데, bino(2,1)가 두 번 호출된다.
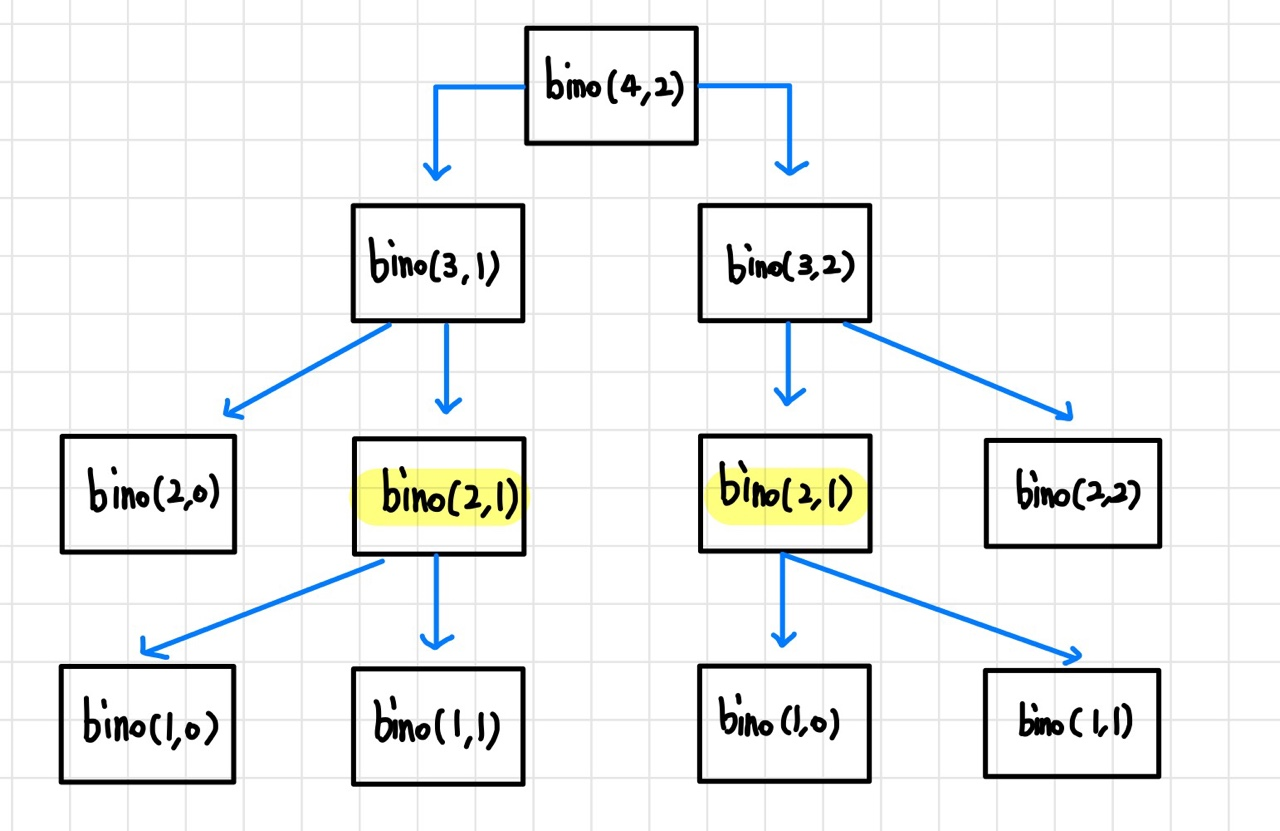
- 또한 bino(2,1)을 통해 bino(1,1)와 bino(1,0) 각각 2번씩 중복되어 호출되고 있다.
- 그래서 중복된 함수 호출을 제거한다면 아래와 같은 그림이 나온다.

- 그러나, 아무리 중복을 제거한다고 해도 n과 r이 커짐에 따라 결국은 함수의 중복 호출 수는
기하급수적으로 증가하게 된다.
- 이러한 해결을 위해서는 동적 계획법에서 말하는 캐시(cache)를 이용하는 것이다.
- 즉, 입력인 n과 r이 정해져 있을 때 bino(n,r)의 반환 값이 일정하다는 사실을 이용하면, 캐시를 사용해
이 문제에서 중복 계산을 제거할 수 있다는 것이다.
- 방법은 함수로 매번 호출될 때마다 캐시에 접근해 값이 저장되어 있는지를 확인한 뒤, 저장되어 있다면
이것을 즉시 반환한다.
( 이것을 메모이제이션(memoization)이라고 부르는 데, 함수의 결과를 저장하는 장소를 마련해 두고, 한 번
계산한 값을 저장해 뒀다 활용하는 최적화 기법이다. )
- 아래의 코드는 메모이제이션을 이용한 이항 계수의 계산이다.
|
// 캐시 배열을 0으로 초기화
int[][] cache = new int[30][30];
int bino2(int n, int r) {
// 기저 사례(1): 뽑아야 하는 수가 0 이거나 뽑히는 원소의 개수와 뽑는 개수가 같으면 1 반환
if(r==0 || n==r) return 1;
// 0이 아니라면 한 번 계산했던 값이니 곧장 반환
if(cache[n][r] != 0) return cache[n][r];
// 직접 계산한 뒤 배열에 저장
return cache[n][r] = bino(n-1,r-1) + bino(n-1,r);
}
|
- 아래의 호출 횟수 표처럼 bino1()보다 bino2()가 더 상당히 적게 호출하는 것을 볼 수 있다.
| n | 2 | 3 | 4 | 5 | ... | 18 | 19 | ... | 25 |
| bino1() | 3 | 5 | 11 | 19 | ... | 97239 | 184755 | ... | 10400599 |
| bino2() | 3 | 5 | 8 | 11 | ... | 99 | 109 | ... | 181 |
3. 메모이제이션을 적용할 수 있는 경우
- 메모이제이션은 *참조적 투명 함수의 경우에만 가능하다.
( *참조적 투명 함수는 입력이 고정되어 있을 때 그 결과가 항상 같은 함수들을 말한다. )
( 또한 참조적 투명성은 함수의 반환 값이 입력 값만으로 결정되는지의 여부를 뜻한다. )
4. 메모이제이션의 시간 복잡도
- 메모이제이션을 사용하는 알고리즘의 시간 복잡도는 간단하게 아래와 같은 식을 이용하여 주먹구구로
계산할 수 있다.
( 존재하는 부분 문제의 수 ) X ( 한 부분 문제를 풀 때 필요한 반복문의 수행 횟수 )
- 예를 들어, bino2()의 시간 복잡도 계산해보면, "O(N^2) X O(1) = O(N^2)" 이 나오게 된다.
- 단, 존재하는 부분 문제의 수는 캐시에서 찾을 수 있는 것이 많이 있기 때문에, 실제로 O(N^2)보다
수행시간이 더 작을 수 있다.
'알고리즘 (with JAVA) > 기본 알고리즘' 카테고리의 다른 글
| 선택 정렬 (Selection Sort) (0) | 2023.04.27 |
|---|---|
| 퀵 정렬 (Quick Sort) (0) | 2023.04.27 |
| 거품 정렬 (Bubble Sort) (0) | 2023.04.27 |
| 안정 정렬과 불안정 정렬 (0) | 2023.04.27 |
| 탐욕법 (Greedy Method) (0) | 2022.10.17 |