폴리오미노 (난이도: 중)
1. 문제 설명
(1) 정사각형들의 변들을 서로 완전하게 붙여 만든 도형들을 폴리오미노(Polyomino)라고 부른다.
(2) N개의 정사각형으로 구성된 폴리오미노들을 만들려고 하는데, 이 중 세로로 단조(monotone)인
폴리오미노의 수가 몇 개나 되는지 세고 싶다.
* 세로로 단조라는 뜻은 어떤 가로줄도 폴리오미노를 두 번 이상 교차하지 않는다는 것이다.
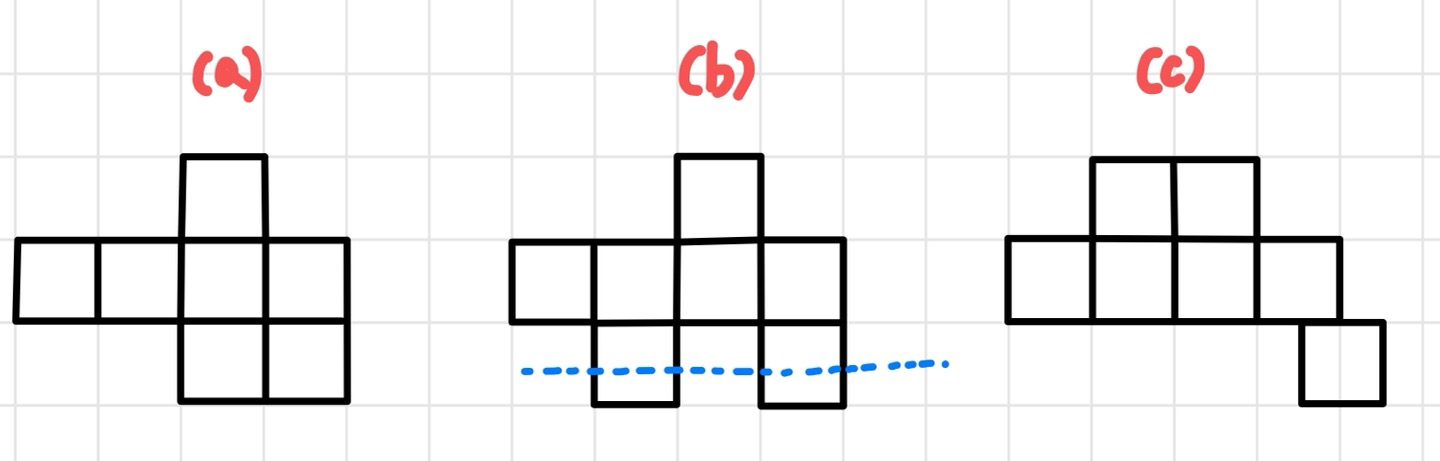
(3) 예를 들어, 아래의 그림 (a)는 정상적인 세로 단조 폴리오미노이지만, (b)는 파란색 점선이
폴리오미노를 두 번 교차하기 때문에 세로 단조 폴리오미노가 아니다.
* (c)는 맨 오른쪽 아래 사각형이 변을 완전히 맞대고 있지 않기 때문에 폴리오미노가 아니다.
(4) N개의 정사각형으로 구성된 세로 단조 폴리오미노의 개수를 세는 프로그램을 작성하시오.
2. 입출력 조건 및 예제
입력 조건
(1) 입력의 첫 줄에는 테스트 케이스의 수 C(1<=C<=50)
(2) 폴리오미노를 구성할 정사각형의 수 N(1<=N<=100)
출력 조건
(1) 각 테스트 케이스마다 N개의 정사각형으로 구성된 세로 단조 폴리오미노의 수를 출력
* 만약 폴리오미노의 수가 10,000,000 이상일 경우 10,000,000으로 나눈 나머지 출력
입력 예제
3
2
4
92
출력 예제
2
19
4841817
3. 제약 조건
(1) 프로그램은 1초 안에 실행되어야 하며, 64MB 이하의 메모리를 사용해야 한다.
4. 가정법
X
5. 기저 사례
X
6. 코드 및 풀이
: 완전 탐색으로 시작한다.
먼저 우리가 세어야 하는 폴리오미노는 세로 단조이다.
그러므로 각 가로줄에 포함된 정사각형들은 항상 일렬로 연속해 있다는 사실을 알 수 있다.
그렇다면 첫 번째 가로줄에 포함된 정사각형의 수를 기준으로 분류하여 모든 폴리오미노를 세어본다.
그러나 이들의 경우의 수를 세어보면 그렇게 단순하지는 않다는 것을 알 수 있다.
예를 들어, 첫 번째 줄과 두 번째 줄에 모두 두 개의 사각형이 존재한다면, 아래의 그림과 같이 세 가지의 경우가 존재한다.

반면 첫 번째 줄에 하나의 사각형만 들어간다면, 아래의 그림과 같이 두 가지 방법으로밖에 붙일 수 밖에 없다.

그렇기 때문에, 아래의 그림처럼 나머지 사각형으로 만든 폴리오미노의 첫 번째 줄에 있는 정사각형의 수 별로
폴리오미노의 수를 반환할 수 있는 부분 문제가 존재해야 한다.

* n개의 정사각형을 포함하되, 첫 줄에 first개의 정사각형이 들어가는 폴리오미노의 수
이때 poly(n,first)를 구하는 방법은 첫 줄에 들어가야 하는 정사각형이 정해져 있으니 아래의 그림처럼
n-first개의 남은 정사각형들을 계산하는 것이다.

이때 두 번째 줄에 있는 정사각형의 수에 따라 이들을 붙일 수 있는 방법의 수가 정해진다.
예를 들어, N이 9이고 first가 2라고 가정하고 아래의 그림과 같이 폴리오미노를 있다고 하자.

그러면 맨 윗 줄과 이 폴리오미노를 다음과 같이 4가지 형태로 붙일 수 있을 것이다.

이것을 일반화하면 첫 줄에 first개의 정사각형이 있고, 나머지 사각형으로 만든 폴리오미노의 첫 줄에
second개의 정사각형이 있다고 할 때 이들을 붙일 수 있는 방법의 수는 (first + second -1)임을 알 수 있다.
따라서 위 식의 각 항마다 폴리오미노들을 붙일 수 있는 방법의 수를 곱해 주면 아래의 그림에 있는 수식을
얻을 수 있다.

* N과 first는 각각 [0, 100] 범위 내의 정수이므로 쉽게 메모제이션이 가능하다.
점화식은 아래 7. 점화식에 있다.
public class Polyomino {
private static BufferedReader sc = new BufferedReader(new InputStreamReader(System.in));
private static StringBuilder sb = new StringBuilder();
private static int N;
private static int MOD = 10*1000*1000;
private static int[][] cache;
public static void main(String[] args) throws IOException {
StringTokenizer st;
int C = Integer.parseInt(sc.readLine());
for(int i=0; i<C; i++) {
cache = new int[101][101];
N = Integer.parseInt(sc.readLine());
// 맨 윗줄부터 1개, 2개, ... , N개까지
// 놓는 경우의 수를 세기 위해 j<=N까지
int result=0;
for(int j=1; j<=N; j++) {
result += solve(N, j);
}
sb.append(result%MOD+"\n");
}
System.out.println(sb);
}
private static int solve(int n, int first) {
if(n==first) return 1;
if(cache[n][first]!=0) return cache[n][first];
int ret=0;
for(int second=1; second<=n-first; second++) {
int add = second+first-1;
add *= solve(n-first, second);
add %= MOD;
ret += add;
ret %= MOD;
}
return cache[n][first] = ret;
}
}
7. 점화식

8. 시간 복잡도
- 가능한 N과 first의 조합수는 O(N^2)이고 poly()를 한 번 계산하는 데는 O(N) 시간이 발생하기 때문에,
전체 시간 복잡도는 O(N^3)이 된다.